VOLUMENES DE TIERRA EN URBANIZACIONES
diciembre 12, 2020VOLUMENES DE TIERRA EN URBANIZACIONES
VOLUMENES DE TIERRA O TERRACERIA
El trabajo de calcular volúmenes de tierra
- Para efecto de costeo
- Para efecto de establecer una superficie predeterminada de cualquier obra que se requiera efectuar
METODOS DE CUBICACION EN TERRACERIA
La medición directa de volúmenes de tierra rara vez se efectúan en topografía, si no que se emplean en mediciones indirectas determinando las curvas de nivel y areas que tengan relacion con el volumen deseado
VOLUMENES DE TIERRA O TERRACERIA
Se utilizan 4 procedimientos principales
- El método de curvas de nivel
- El método de área base por la altura
- El método de uso de perfiles
- Método de usos de las secciones transversales
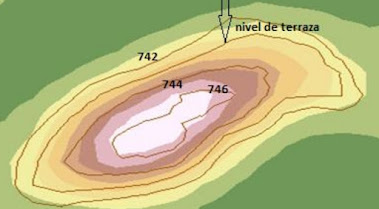
- Como una alternativa para la determinación de volumenes por medio de las secciones transversales, es posible calcular el volumen usando las areas horizontales contenidas por curvas de nivel.
- Los volumenes basado en curvas de nivel se obtienen a partir de planos topográficos planímetros, la superficie limite por cada curva de nivel y multiplicando el promedio de las areas por la equidistancias entre dichas curvas de nivel.
VOLUMENES DE TIERRAS O TERRACERIA
METODO DE AREA BASE POR ALTURA
El calculo de un volumen por este método resulta fácil si se conoce las elevaciones de los determinados puntos que forman una figura sencilla tales como triángulos ,cuadrados, rectángulos, trapecios etc.
METODO DE AREA BASE POR ALTURA
Así: 𝑉 = 𝐴 ℎ1+ℎ2+ℎ3 3 si la base es un triangulo
𝑉 = 𝐴 ℎ1+ℎ2+ℎ3+ℎ4 4 Si la base es un rectángulo
VOLUMENES POR ALTURA DE PUNTOS
- Este método para determinar volúmenes es especialmente útil en la determinación de volúmenes para grandes excavaciones abiertas para tanques, áreas de material , etc y para operaciones de nivelación tal como campos de juego o sitios de construcción.
- Se puede aplicar también en la determinación de volúmenes de desperdicios. Habiéndose localizado la línea exterior de la estructura sobre el terreno, el ing. o Arq. debe de dividir el área en cuadros o rectángulos, marcando las esquinas y posteriormente tomar lecturas de nivel sobre estas.
- El tamaño de los cuadros dependerá de la naturaleza del terreno; las esquinas deberán estar lo suficientemente cercanas para considerar la superficie del terreno entre las líneas como un plano restando el nivel observado del correspondiente
VOLUMENES POR ALTURA DE PUNTOS
Restando el nivel observando del correspondiente nivel del proyecto, se obtiene una serie de alturas de las curvas se puede determinar el volumen de cada cuadro como el área plana plana multiplicanda por el promedio de las profundidades de excavaciones (0 rellenos) en las cuatro esquinas.
Cota de excavación de la terraza es de 714MS
En los cuadros A,B,C,D
Vol. de cada = Hpromx Área de la base
PARA RESOLVER
VOL. DE CADA PRISMA= HpromXArea la base
Prisma A diferencia de cotas
(743.1-714)+(734.8-714)+(727.3-714)+(737.2-714)
Hprom= (29.1+20.8+13.3+23.2)/4= 21.6
Prisma B
(734.8-714)+(727.3-714)+(717.4-714)+(727.3-714)
Hprom=(20.8+13.3+3.4+13.3)/4=12.7
Prisma C
(737.2-714)+(727.3-714)+(722.5-714)+(729.3-714)
Hprm =(23.2+13.3+8.5+15.3)/4 =15.075
Prisma D
(727.3-714)+(717.4-714)+(714.3-714)+(722.5-714)
Hpro = (13.3+3.4+0.3+8.5)/4 = 6.375
Hprom = (21.6+12.7+15.075+6.375)/4= 13.9375 mts
Vol. De cada prisma= HpromxArea de la base
Vol=00*21.6+100*12.7+100*15.075+100*6.375=5575 mts3
vol. =20*20*13.9375=5575 mts3
MÉTODO A TRAVÉS DE LA FRECUENCIA
Este método consiste en verificar cuantas figuras geométricas llegan a cada vértice
Así nivel terraza: =714
Forma de anotar y poder obtener el volumen:
Hprm=∑prod/∑frecuencia
Hprm=223./16=13.9375 mts
Vol=hpromxArea
Vol= 13.9375x20x20
Vol;= 5575 mts3
CUANDO TENEMOS CURVAS DE NIVEL
Cuando se tiene en un terreno solo las curvas de nivel y queremos calcular los volumenes de tierra de una sección donde se piensa realizar una construcción, se tiene que realizar una interpolación para poder obtener las elevaciones del área que se va a necesitar obtener dichos volumenes.
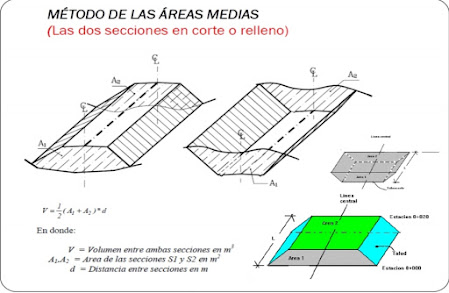
METODO DEL PERFIL
A partir del perfil de los proyectos se hayan las profundidades promedios de las secciones transversales para la cual se mide con planímetro o con cualquier figura geométrica
CONDICIONES PARA APLICAR EL METODO
- En la sección de corte de relleno, considera el terreno que es de un mismo nivel.
- La altura media se considera igual.
- El ángulo de inclinación se considera de 45°
hcm= altura de corte medio
𝐻𝑐 =
Σ𝐴𝑐
Σ𝐿𝑐
=
𝐴1𝑐+𝐴2𝑐+𝐴3𝑐
𝐿1𝑐+𝐿2𝑐+𝐿3𝑐
𝐴𝑚 = 𝐵 + 𝐻𝑐𝑚 ∗ 𝐻𝑐𝑚
De igual forma cuando es una sección de relleno
HMR=
Σ𝐴𝑟
Σ𝐿𝑟
=
𝐴1𝑟+𝐴2𝑟+𝐴3𝑟+..
𝐿𝑟1+𝐿𝑟2+𝐿𝑟3+👉𝐴𝑚𝑟 = 𝐵 + 𝐻𝑟𝑚 𝐻𝑟𝑚
El volumen V=A*L
V Relleno= AMR*ΣLR Volumen en banco
V Corte= AMC*∑LC
Existen varios métodos para determinar los volumenes, el mas practico para proyecto de carrera es aquel que se calcula entre 2 secciones transversales consecutivas, multiplicando por la distancia que lo separa
El volumen será 𝑉 = 𝐿( 𝐴1+𝐴2 2 ) L= Distancia entre las 2 secciones, A1= Área de la seccion1 A2= Área de la sección 2
Y cuando las 2 secciones tienda a 0 el volumen se calcula así:
V = 1 3 ∗ A ∗ L
CALCULO DE VOLÚMENES DE TIERRA
cuando deseamos una mayor precisión o el valor de las 2 áreas el valor de las 2 áreas es muy diferente entre si, se calcula el volumen como si fuera un prismoide
así 𝑉𝑜𝑙 = 𝐿 6 ∗ (𝐴1 + 4𝐴𝑚 + 𝐴2)
AM = Área media, pero cuando solo tenemos los promedios se le puede corregir por la formula de la corrección así: 𝐶 = 1.68(𝐻𝑜 − 𝐻1)(𝐷𝑜 − 𝐷1) DONDE C= Corrección para un prismoide.
EJEMPLO A RESOLVER:
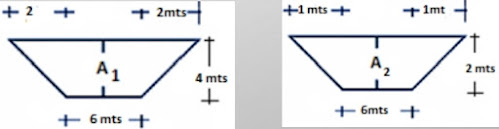
Calcular el volumen entre las dos secciones aplicando los métodos distancias entre estaciones es de 20mts.
- Formula de los promedios
- Formula de prismoide
- Formula por corrección
Ejemplo a resolver: Calcular el volumen entre las dos secciones aplicando los métodos. Distancia entre estaciones es de 20 mts.
A1=(6+10 2 )X4 = 32 MTS2
A2=(6+8 2 )X2 = 14 MTS2
AM=(6+9 2 )X3 = 22.5 MTS2
FORMULA DE LOS PROMEDIOS
𝑉 = 𝐿( 𝐴1+𝐴2 2 ) 𝑉 = 20( 32+14 2 )= 460MTS3
FORMULA DEL PRISMOIDE
𝑉𝑜𝑙 = 𝐿 6 ∗ (𝐴1 + 4𝐴𝑚 + 𝐴2) así 𝑉𝑜𝑙 = 20 6 ∗ 32 + 4 22.5 + 14 = 453.3 𝑀3
FORMULA POR CORRECCIÓN
𝐶 = 1.68 𝐻𝑜 − 𝐻1 𝐷𝑜 − 𝐷1 𝐶 = 1.68(4 − 2)(10 − 8) = 6.72 M3
HAY QUE AJUSTAR AL CALCULO DE LOS PROMEDIOS ASI
V= (460 – 6.72) M3 2
VOL = 453.28
- Formula de los promedios
- Formula del prismoide
- Formula por corrección























0 comentarios