LADOS DE LIGA Y ERROR PROBABLE
octubre 27, 2020Este método es utilizado cuando el terreno es encerrado por un polígono y es de tal naturaleza que no permiten el empleo de los métodos anteriores por que existen obstáculos que impiden ver tres vértices consecutivos del polígono base.
Métodos de lados de liga: se mide a , b , c , en cada vértice ; donde b es el “lado de liga "y el ángulo se calcula así:
PROCEDIMIENTO PARA LADO DE LIGA
Esto se realiza en cada vértice se mide una distancia atrás y otra adelante que sea igual veamos:
Comprobación de los ángulos internos
∑‹ inter = 180 (n-2)
∑‹ exter = 180 (n+2)
Donde:
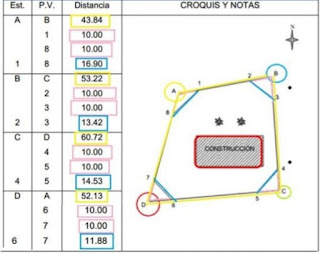
SOLUCION DEL EJERCISIO
Cálculos de los ángulos internos:
A=2ARC Sen 116.90/2(10) =115˚20’37.94”
B=2ARC Sen 13.42/2(10)= 84˚17’18.9”
C=2ARC Sen 14.53/2(10)=93˚11’15.17”
D=2ARC Sen 11.88/2(10)=72˚52’57.92”
SUMATORIA= 365˚42’9.93”
Encontrar la tolerancia y error angular
T= 0.5˚√n = 0.5*√4= 1˚00’00”
∑<int=180(n-2) = 180(4-2)= 360˚00’00”
E <=365˚42’9.53” - 360˚00’00”= 5˚42’9.53”
por lo tanto la t es mayor E< :;
no se puede compensar, a pesar de esto lo haremos
Comp. Angular= 5˚42’9.53”/4=1˚25’32.38”
-1˚25’32.38”=113˚ 55’5.56”
-1˚25’32.38”=82˚51’46.52”
-1˚25’32.38”=91˚45’42.79”
-1˚25’32.38”=71˚27’25.54”
Después de realizar todo el proceso de calculo de los ángulos se procede a calcular el área y si nos piden el área de Ha, A, Ca, y Mz y Vrs2
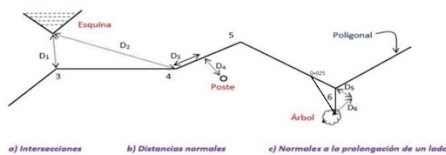
LEVANTAMIENTO DE DETALLES
Se fijan por intersección, es decir por medio de dos distancias o por medio de los lados del polígono base o sus prolongaciones. así, ejemplo:
MEDICION EN TERRENOS PLANOS
Para llevar a cabo la medición hay que seguir los tres pasos descritos a continuación.
- ALINEACIÓN: La línea a medirse se marca en forma definida en ambos extremos y también en puntos intermedios, si fuera necesario, para asegurarse de que no hay obstrucciones a las visuales. Esto se hace con los jalones, el cadenero delantero es alineado en su posición por el cadenero trasero. Las indicaciones se dan a voces o por señales con las manos.
- TENSADO: El cadenero trasero sostiene el extremo de la cinta sobre el 1er. Punto (el de partida) y el cadenero delantero que sostiene el extremo con la marca cero, es alineado por aquel. Para obtener resultados exactos, la cinta debe estar en línea recta y los dos extremos sostenidos a la misma altura. Se aplica entonces una tensión específica para mantener la cinta lo más horizontal y sin ondulaciones.
- MARCAJE: Una vez alineada y tensada correctamente la cinta, estando el cadenero trasero en el punto inicial da la señal de listo; el cadenero delantero clava un jalón, el jalón debe clavarse en posición perpendicular a la cinta.
Cuando no se puede mantener la cinta horizontal debido a la inclinación del terreno hay dos posibles métodos según el grado de inclinación.
1. Si la inclinación del terreno no es mucha se puede hacer mediante el método de banqueo.
2. Si la inclinación es excesiva se puede hacer mediante la medición usando la corrección por pendiente o sea tomar la distancia horizontal transformarla a distancia inclinada y medir con la cinta.
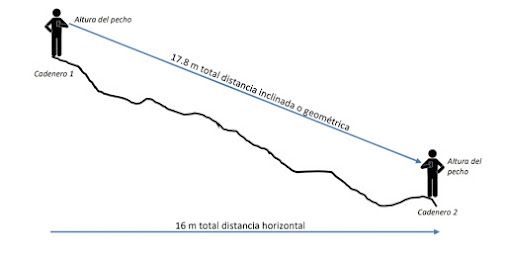
En declives o terrenos inclinados cuando no se puede mantener la cinta horizontal en una distancia de 30 mts. Se mide por tramos parciales horizontales que se van sumando hasta totalizar una longitud completa de la cinta. Para los tramos a elegirse deberá considerar que la cinta no sobrepase la altura del pecho.
EJEMPLO: Supóngase que cuando se sostiene el extremo de 30 m de la cinta en el punto inicial, el cadenero delantero solo puede avanzar 9 m cada vez sin que sobrepase su altura mayor que la del pecho. En tales condiciones, clava una estaca o marca bajo la medida de 21 m como se muestra en la figura.
El cadenero trasero avanza hasta la señal indicada y sostiene ahí la graduación de 21 m. mientras el otro clava otra marca, por ejemplo en la marca de 7 m finalmente con la graduación de 7 m. sobre la segunda ficha, se marcan la distancia que completa los 30 m. con un punto cero. Se recomienda medir cuesta abajo y no en pendiente arriba.
METODO POR CORRECION DE PENDIENTE
Cuando la inclinación o pendiente es mucha entonces es mejor convertir la distancia horizontal en distancia inclinada (geométrica) y realizar la medición siguiendo las debidas reglas (Cinta tensa, sostener los extremos a la altura del pecho o similar altura de los cadeneros, etc.)
MEDICION EN TERRENO INCLINADO O CON PENDIENTE
Este método es mas exacto y rápido que tratar de sostener la cinta horizontalmente y bajar los puntos al terreno con plomada. La única diferencia entre este método y el de medición sobre un terreno plano es que se debe aplicar una corrección cuya magnitud hay que considerarla.Resulta evidente que el valor de la corrección ”cp” es la diferencia entre s y h. la relación de los lados v/h se denomina pendiente. según se vio la corrección cp es igual ala diferencia s-h, que puede deducirse del triangulo rectángulo así:
s 2 =h2 + v2 v 2 = s2 – h 2 (s – h)( s+ h) = v2 s – h = v2 /s+h
y como s-h = cp se tiene cp= v2 /s+h = v2 /2s
TEORIA DEL ERROR
Es la diferencia entre una medición y el valor verdadero de la cantidad medida y es el verdadero error de esta medición.
CAUSAS DE LOS ERRORES:
- Instrumentales debido a las imperfecciones de los aparatos
- Naturales, la temperatura, el viento
- Personales. Debido a las pocas habilidades, inexperiencias del que lee y opera el aparato.
VALOR PROBABLE
El valor mas probable de una cantidad medida varias veces es el promedio de las medidas tomadas o la media aritmética. esto aplica tanto en ángulo como en distancia y desniveles.
- VARIAS MEDIDAS DE LA MISMA CANTIDAD. tres medidas se han hecho de una línea con igual cuidado y son: 160.01, 160.10 y 160.03. por lo tanto el valor más probable es 160.047.
- MEDIDA DE VARIAS CANTIDADES HOMOGÉNEAS. cuando se trata de magnitudes de igual. ej. la suma de los tres ángulos de un triangulo es 179º59’, se sabe que el valor exacto de la suma de los ángulos de un triangulo es 180º, el error verdadero es 1’ o sea 60’’.
Si 25.27 MT. Es la medida de varias mediciones y 0.09 Es el error probable del valor medio, Existe la misma probabilidad para que el verdadero valor se halle entre:
VALOR PROBABLE PARA LA MISMA CANTIDAD
El V.P. de una magnitud medida varias veces en las mismas condiciones es la media aritmética de todas las mediciones hechas. Nota: es la media aritmética de todas las mediciones admitidas como probables.
N: Numero de Observaciones:
EJEMPLO = Las mediciones de una longitud han dado como resultado:
854.21,854.27,854.22,856.25, 854.26 mts
Indica el grado de precisión que cabe esperar en una sola observación, hecha en las mismas condiciones que las demás
0.6745 : Constante de proporcionalidad∑(x-x)2 = v2 = Errores residuales
N = Números de observaciones
ERROR PROBABLE DE LA MEDIA ARITMÉTICA
De un cierto numero de observaciones de la misma cantidad será:
ERROR RELATIVO
Es la forma unitaria de expresar el error, dando así mejor significado de la precisión de las mediciones. Se expresa en forma de una fracción siendo el numerador la unidad así:
El error probable de la media aritmética sirve para expresar la fluctuación que pude tener el valor promedio entonces tenemos:
VALOR MAS PROBABLE :V.M.P.
EJEMPLO:
Calcular la altura de un punto que se realizo 12 mediciones usando un nivel fijo y se realizaron en igualdad de condiciones obtenidas:
2.187,2.182,2.179,2.181,2.184,2.176,2.186,2.183,2.178,2.181,2.188,2.179, Calcular:
- Error probable de una sola medición
- Error probable de todas las mediciones
- Error relativo
- Valor mas probable
Valor mas probable
VMP= 2.182 + 0.000728 = 2.182728
VMP= 2.182 – 0.000728 = 2.181272
PRACTICA #1 Y #2
👀 Apuntes de clases
VIDEOS RECOMENDADOS
https://www.youtube.com/watch?v=AiAJAEz3w1Q
https://www.youtube.com/watch?v=PxvrUEEFyXo












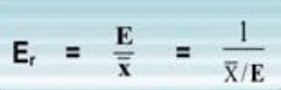




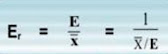






0 comentarios