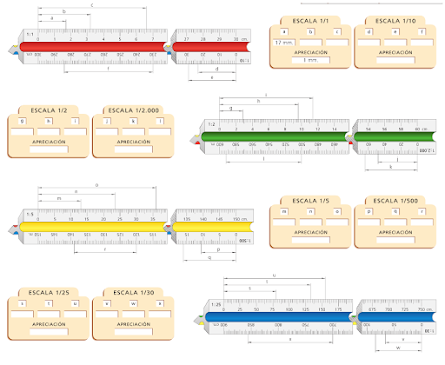
TIPO DE ESCALAS

LEVANTAMIENTO CON CINTA DE UN TERRENO

ESCALAS

Se denomina escala (E) a la relacion constante que existe entre una longitud medida en un plano (P) y la correspondiente longitud medida en el terreno (T); expresada como una formula de la siguiente manera.

Escala: Dimensiones en la carta, mapa o plano
                     Dimensiones en el terreno
Escala= Papel =    P
              Terreno    T

CLASES DE ESCALAS

La escala de un plano puede ser Grafica o Numérica, la escala numérica a su vez puede ser de dos clases:

• Con unidades denominadas escala verbal.
• Sin unidades llamada también escala fraccionaria.

ESCALA FRACCIONARIA

Se representa como su nombre lo indica por una fracción, cuyo numerador es la unidad y su denominador las unidades tomadas en el plano. 
Ejemplo: 1/500  1/1000  1/2000 etc.

Quiere decir esto que una unidad de medida en plano o mapa representa D (denominador) unidad medida en el terreno. o sea: E = 1/D

Según la definición establecida y representada por la formula anterior E = P/T la igualamos y tenemos:

1/D = P/T  de donde  T = PXD

En esta nueva formula T representa las unidades medidas en el terreno, P las unidades medidas en el plano y el D el denominador de la escala. 

EJEMPLO:

• Cuantos centímetros medirá en un plano o mapa a una escala de 1:50000 una linea que en el terreno mide 8500mts.

• En un mapa cuya escala es 1:20000 se determina la longitud de una linea, siendo esta 8.4 cm. cual será la longitud de esta linea en el terreno.

ESCALA COMERCIAL

En el mercado profesional se utilizan principalmente los siguientes escalas: 1:1 , 1:2 , 1:2.5 , 1:5 , 1:7.5 , 1:12.5 

Así como múltiplos de estas así: 1:10 , 1:1000 , 1:20, 200 , 1:2000
Las escalas se pueden denominar: 

• Grandes: Cuando el denominador esta entre 2 y 25000

• Mediana: 250000 500000

• Pequeña: es un valor mayor de 500000

ESCALAS GRAFICAS

La escala grafica consiste en una linea recta (llamada linea portadora) dividida en distancia correspondiente a determinado numero de unidad de longitud del terreno

TIPOS DE EDCALAS

                                      Escala Natural                  Escala de Ampliación          Escala de Reducción

CLASES DE CINTA

Una cinta métrica es la reproducción de un numero determinado de veces (3,5,30,50,100) de la unidad patrón.
En el proceso de medida, las cintas son sometidas a diferentes tensiones y temperaturas, por lo que dependiendo del material con el q ha sido construida, su tamaño original variara. Por esta razón las cintas viene calibradas de fabricas para que a una temperatura, tensión y condición de apoyo dadas, su longitud sea igual a la longitud nominal.

Las cintas métricas empleadas en trabajos topográficos deben ser de acero, resistentes a esfuerzos de tensión y a la corrosión comúnmente, las cintas métricas vienen en longitudes de 30, 50, 100m, con una sección transversal de 8mm x 0,45mm para trabajos fuertes en condiciones severas o de 6mm x 0,30mm para trabajo en condiciones normales.

RECOMENDACIONES PARA EL USO DE CINTA

• Antes de efectuar una medición verificar el estado de la cinta.

• Si se usa cinta con carrete tener la seguridad que la cinta enrolle con facilidad 

• Que los números sean visibles

• Después de usar limpiar la cinta

• Al usar la cinta en calles transitadas hay que tener el cuidado que no le pasen las llantas

ERRORES EN LA MEDICION CON CINTA

• La longitud de la cinta esta errónea

• La alineación imperfecta

• Falta de horizontalidad de la cinta

• Cinta floja o torcida

• Variación de tensión

PRESICION EN LA MEDICION CON CINTA

Si la medición se efectúa sin ampliar la tensión suficiente no son muy experto en mantener cadeneros no son muy expertos en mantener dentro de ciertos limites razonables, la horizontalidad de la cinta, la precisión puede ser baja.

ERRORES EN LA MEDICION CON CINTA

Equivocaciones que se presentan al medir:

• Añadir o quitar un tramo de cinta

• Añadir o quitar un metro o quitar

• tomar como ¨0¨ (cero) o como 30 una porción equivocada

• Lecturas incorrectas de los números 6 y 9 decir los números incorrectamente

LEVANTAMIENTO DE UN TERRENO CON CINTA

Cuando se va a levantar áreas relativas pequeñas se pueden utilizar la cinta. El principio utilizado es el de subdividir el área dada en figuras como triángulos, rectángulos, etc

Lo primero que hay que hacer es un reconocimiento del terreno (todo el área). para determinar los sitios mas ventajosos para las estaciones de levantamiento.

Estos puntos deben elegirse cuidadosamente y su elección depende de muy diversos factores. veamos:

• Seleccionar adecuadamente los lados del polígono 

• Tener una distribución en triángulos bien conformados

• Buena condición para las medidas

• Estabilidad y permanencia de las estaciones o mojones

• Estación bien referenciadas

• Visibilidad entre estaciones 

POLIGONO DE BASE TRIANGULAR

Triangulación topográfica Cuando se dispone a realizar un levantamiento de una zona muy extensa, será preciso cubrir dicha zona con una red de triangulación, es decir, una red de puntos cuyas coordenadas consideraremos fijas y en la que podremos apoyar nuestras poligonales o nuestro vuelo.

Esta triangulación consiste en un esqueleto básico compuesto por triángulos donde se apoyarán el resto de métodos topográficos. Será la base del levantamiento, y por lo tanto, deben tomarse cuantas precauciones sean razonables para garantizar su precisión. Esta red de triangulación se realiza generalmente con técnicas GNSS, pero cuando no resulta posible el empleo de estas técnicas, se impone el uso de la topografía clásica.

Si recurrimos a la triangulación clásica, la observación se realizará por el método de vueltas de horizonte, y en aquellos casos en los que se necesite mucha precisión, por el método de pares sobre la referencia.

PROCEDIEMIENTO

• Reconocimiento

• Trazo y medición del polígono base, incluyendo diagonales

• Levantamiento de detalles con relacion al polígono

• Calculo de los ángulos del polígono

• Dibujo de lo levantado

• Calculo del área total

EJEMPLO:

                                                                               Sea: S el área del triángulo
                                                                               Sabemos que: S= a.h
   S= √p(p-a)(p-c)                                                                                   2
                                                                               Pero: h= bSenC
                              
                                                                               Entonces: S= ab SenC
                                                                                                      2
                                                                               Análogamente: 
                                                                               S= bc Sen A    S= ac Sen B
                                                                                     2                      2  

                                           

Área del trapecio : 

                           Área =h a + b  (Siendo a y b las bases y h la altura)

                                            2

Área de un cuadrilátero: 

Area1= ABH= 1/2xAHxBHXsenH 

Area2= BCH= 1/2xBHxCHxsenH 

Area3= CDH= 1/2xCHxDHXsenH 

Area4= DAH= 1/2xDHxAH                                    

En estas formulas:
A, B, C = Ángulos interiores
a, b, c = Lados del triangulo 

Tan 1/2 A = √ (p - b)(p-c)
                          p (p-a)
Tan 1/2 B = √ (p - a)(p-c)
                          p (p-b)
Tan 1/2 C = √ (p - a)(p-b)
                          p (p-c)

OTRAS FORMAS DE OBTENER LOS ANGULOS INTERNOS POR LA LEY DEL COSENO

Cos A = b2+ c2+ a2 de donde a2 =b2+c2-bc  Cos A 

                    2bc
Cos B = a2+ c2+ b2 de donde b2 =a2+c2-2abc  Cos B
                     2ac
Cos C = a2+ b2+ c2 de donde c2 =a2+b2-2ab  Cos C

VIDEOS RECOMENDADOS

https://www.youtube.com/watch?v=xHb3pARMSME

https://www.youtube.com/watch?v=3K2tcYC5nDM

BIBLIOGRAFIA

👀 Apuntes de clases