DIVISION DE TERENOS Y DATOS FALTANTES

DIVISION DE SUPERFICIE

Los problemas que se presentan en la partición de terrenos (fincas, parcelas, etc) son tan variados y numerosos. cuando hay que medir una parcela dada en dos o mas se hace un replanteo, se calculan las coordenadas y se determina el área total del terreno.

PROCEDIMIENTO

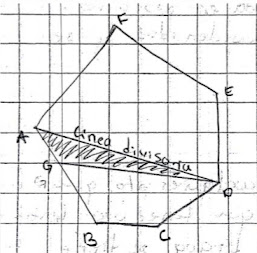
Separar una parte determinada de terreno desde un punto situado en el terreno por medio de una línea cuya dirección no haya sido fijada de antemano. El procedimiento para hallar la dirección y la longitud de la línea divisoria es el siguiente:

• 
  Se traza una linea de "D" a "A" al vértice de la poligonal que queda cerca de la divisoria buscada.

• Se calcula la superficie A, B, C, D, A y se termina la diferencia entre la superficie la deseada y la encontrada. En la figura se supone que la superficie ABCDA es mayor que la deseada y que D,G la posición correcta de la divisoria, por lo tanto el triangulo ADG, representa la superficie en exceso.

• Se calcula la longitud y el rumbo de la linea divisoria AD y el ángulo interno del triangulo ADG.

Se calcula la distancia AG por a siguiente formula: 

• Si nos dan las coordenadas dibujar el polígono a partir de sus coordenadas.

• Si nos dan las coordenadas uno dibujar el polígono a partir de sus coordenadas.

• Se puede obtener sus proyecciones y luego obtener sus rumbos y distancias y con ello poderlo dibujar.

• Con esta información se procede a trabajar la división del terreno con el procedimiento anterior

Y además se dice que la división se tiene que realizar a partir del mojón M05

SOLUCION DE DIVISION DE TERRENOS 

Datos

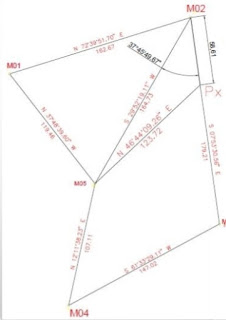
Área buscada = AT/2 =12058.1145 MTS2 = Ab

Obteniendo los cálculos por producto cruzado se obtuvo la siguiente área: 9102.3925 MTS2 obteniendo la diferencia de área que le hace falta para llegar al área deseada es:

AA = 12058.1145 - 9102.3925 = 29.55.722 MTS2 con este dato se obtiene la distancia PX = 2AA / Dist. MO3MO2XSEN0 

Sustituyendo los datos obtenemos PX: 58.60 MTS con esta distancia y el rumbo obtenemos las coordenadas del punto PX a partir de este punto verificamos si tengo el área que ando buscando, lo podemos realizar por producto cruzado.

PROBLEMAS RELATIVOS A DATOS FALTANTES EN POLIGONALES CERRADAS

Cuando por algunas razones no haya sido posible tomar en el campo el RUMBO O LA LONGITUD de todos los lados de una poligonal cerrado se puede en general calcular el dato que falta ya que no puede ser más de dos (UNA LONGITUD, UNA DIRECCIÓN O AMBAS A LA VEZ). 

Si solo falta un dato se puede hacer una comprobación parcial del trabajo. una vez suplida las cantidades que faltaban se puede calcular las coordenadas y dibujarse la poligonal como si no faltara dato alguno de campo. 

Veamos los diferentes problemas que se nos presentan: 

• Falta rumbo y longitud de un lado
• Falta longitud de 2 lados consecutivos 
• Falta longitud de un lado y el rumbo del lado consecutivo

FALTA RUMBO Y LONGITUD DE UN LADO

Calcular las coordenadas de los diferentes vértices de la poligonal a partir de unas coordenadas bases. 

DIST. = L = /(𝑌1 − 𝑌8) 2+(𝑋1 − 𝑋8) 2

RBO= INV.TG 𝑋1−𝑋8 / 𝑌1−𝑌8 

FALTA DE LONGITUD DE 2 LADOS CONSECUTIVOS

En este caso y las siguientes, se pueden resolver calculando la longitud y el rumbo de una línea auxiliar entre los puntos extremos conocidos, formando un triángulo dentro del cual se calculan los elementos faltantes, por la ley del seno o ley coseno. Procedimiento: Calcular las coordenadas de los diferentes vértices de la poligonal Por la línea auxiliar 8-1 se puede obtener el rumbo y la longitud de esa línea. Por diferencia entre los rumbos se obtiene los < en los vértices 8,9,1 Por la ley de los SENOS se obtiene las longitudes 8-9 y 9-1 de esta relación se obtienen las distancias faltantes. 

Procedimiento

Calcular las coordenadas de los diferentes vértices de la poligonal a partir de coordenadas bases 

Por la línea auxiliar se puede obtener el rumbo y la longitud de esa línea 

Conocidos la longitud de los tres lados del triángulo calcular los ángulos internos 5, 6, 1 por cualquier formula: 

SIN 5/2 = (𝑆 − 5 − 6)(𝑆 − 5 − 1) ÷ (5 − 6)(5 − 1) • DONDE : S= (5-6 + 6-1 +5-1)/2 que es el semi perímetro. también aplicando la ley del coseno.

Con los ángulos internos calculados y el rumbo 5- 1 se obtienen los rumbos de 5-6 y 6-1

       

Procedimiento

Calcular las coordenadas de los puntos a partir de una coordenada base por la línea auxiliar (calcular su Long y Rbo ) 

• Por la diferencia de rumbo de la línea 4-5 y 4-1 se obtiene el Angulo interno en 5 . 

• Por la ley del seno obtenemos el ángulo interno en el vértice 5 

• por medio del Rb de 4-5 y el ángulo interno en vértice 4-5 e obtiene el Rb 5-1 

• por diferencia de 180°se obtiene el ángulo interno en 1 

• por ley del seno se obtiene la Dist 4-5